How To Check if a given Binary Tree is Heap.
Hello Friends, In this blog post(Check if a given Binary Tree is Heap) I am going to let you know how to check whether a given binary tree is Heap, BST(Binary Search Tree), Height balanced tree(AVL Tree), complete binary tree, full binary tree?
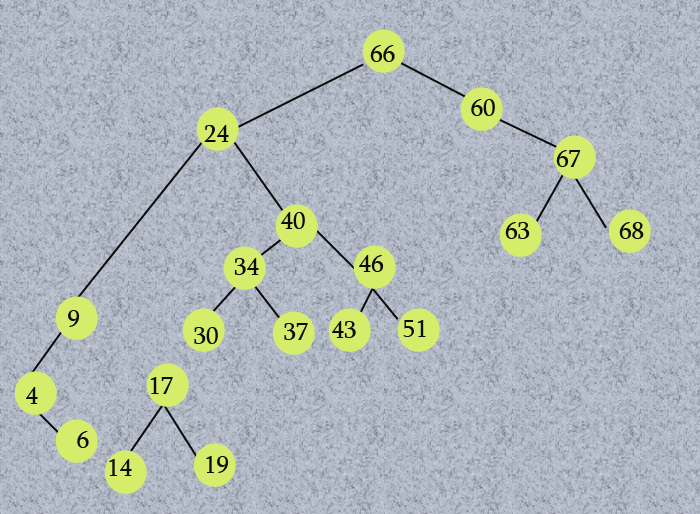
Here we are given a binary tree below, and you have to check what type of binary tree is it. And also need to explain the reason for the same|Check if a given Binary Tree is Heap|
Heap:
Consider the binary tree T in Fig 1. Observe that T is not a heap.
Because neither the largest element in T appears at the top of the heap(max heap) nor the smallest element in T appears at the top of the heap(min-heap).
BST(Binary Search Tree):
Consider the binary T in Fig 1. T is not a binary search tree. Because the 60 and 63 are less than the 66 in its right subtree.
Height Balanced Tree(AVL Tree):
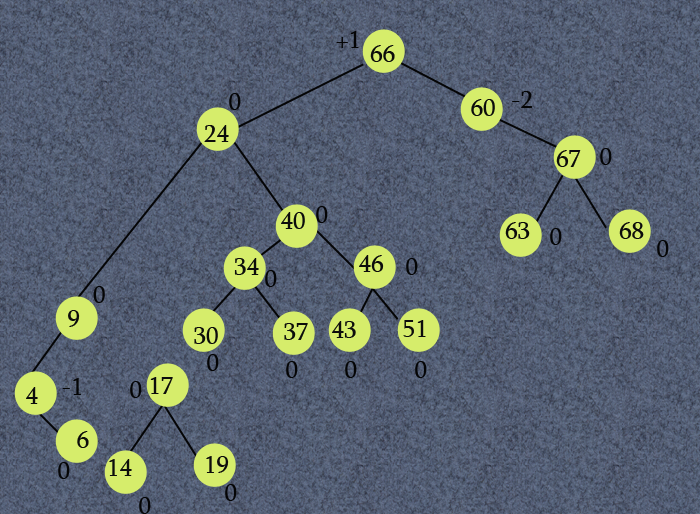
Consider the binary tree T in Fig 1. T is not a height-balanced tree since the balance factor of node 60 is -2.
Each node in a balanced binary tree has a balance of 1, -1, or 0 depending on whether…
… the height of its left subtree is greater than, less than, or equal to the height of its right subtree.
The binary T with all its balance factors is shown in Fig 2 below.
Complete binary tree:
Consider the binary tree T in Fig 1. T is not a complete binary tree.
A complete binary tree is a binary tree whose non-leaf nodes have nonempty left and right subtrees and all leaves are at the same level.
Observe that all leaves are not at the same level in Fig 1.
Full Binary Tree:
Consider the binary tree T in Fig 1.
T is not a binary tree. Since, in a full binary tree, every non-leaf node has a nonempty left and right subtree.
Observe that node 60 and node 4 have no left child.
You can also go through below extensive blog post below.
Difference Between Tree And Binary Tree In Hindi. General tree और binary tree में अंतर हिंदी में |
Please go through the below extensive blog link related to Data Structure:
Sorting Algorithm And Their Time Complexity In Data Structure.
What is meant by the Shell sort in data structure?
Radix Sort In Data Structure / What is the Radix sort used for?
What is a quick sort of data structure?/ How do you write a quick sort?
Selection Sort In Hindi In Data Structure/ How do you perform a selection sort? / Selection sort kya hai?
Bubble Sort In Hindi In Data Structure/ What is bubble sort for example?/ Bubble Sort Kya Hai?
Insertion Sort In Hindi/ insertion sort step by step/ Insertion sort kya hai?
Searching In Data Structure/ What is the searching in data structure?
Shell Sort In Data Structure In Hindi?
Quick Sort In Data Structure In Hindi?
Types Of Data Structure In Hindi…
Tower Of Hanoi In Data Structure In Hindi…
Circular Linked List In Hindi…
Linked list in Hindi…
Data Structure In Hindi…
Dijkstra Shortest Path Algorithm In Hindi…
Heap In Data Structure In Hindi…
Check if a given Binary Tree is a Heap…
B-Tree Example In Data Structure…
Kruskal Algorithm In Hindi In Data Structure…
Prim’s Algorithm In Hindi In Data Structure…
Difference Between Tree And Binary Tree In Hindi…
STACK In Hindi/ STACK Kya Hota Hai…
In the case of any queries, you can write to us at a5theorys@gmail.com we will get back to you ASAP.
Hope! you would have enjoyed this post about how to check whether the given binary tree is a heap, binary search tree, AVL tree, complete binary tree, or full binary tree.
Please feel free to give your important feedback in the comment section below.
Have a great time! Sayonara!


