What is a strongly connected graph?
In this blog post(What is a strongly connected graph), I am going to discuss a strongly connected graph. As we have learned about various types of graphs in our previous blog. We read about the directed graph where each edge is within an ordered pair of vertices means that the first element of this ordered pair is referred to as the starting vertex whereas the second element is known as the end vertex.
In this blog post(What is a strongly connected graph), we will explore How do you know if a graph is strongly connected. What is a strongly and weakly connected graph? How do you create a strongly connected graph? What is the number of strongly connected components in this graph? Strongly connected graph example.
What is a strongly and weakly connected graph?
The graph is called a strongly connected graph if for every pair of vertices(u,v) there is a path between each other, say we should have a path from u to v and v to u. A weakly connected graph is a graph where no path exists between any two pairs of vertices.
How do you create a strongly connected graph?
For making a strongly connected graph we must have a minimum of one in-degree and one out-degree for all the vertices. This means that each vertex must have one incoming edge and one outgoing edge.
Is an empty graph connected?
As we know a null graph is a graph that does not have any nodes, and an empty graph is a graph that does not have an edge. an empty graph of two vertices is not connected.
If a graph is connected and if any two vertices can be connected by a path then a null graph is connected.
We gave you a small reminder of a directed graph as the definition of a strongly connected graph is related to a directed graph.
A directed graph G is said to be connected, or strongly connected if for each pair u, v of a node in G there is a path from u to v and there is also a path from v to u.
On the other hand, G is said to be unilaterally connected if for any pair u,v of node G there is a path from u to v or a path from v to u.
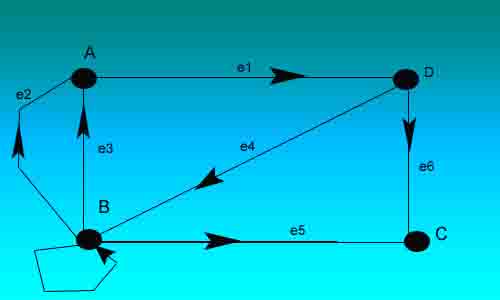
Fig 1 shows a directed graph G with 4 nodes and 7(directed) edges. the edges e2 and e3 are said to be parallel since each begins and ends at the same point B.
The sequence P1 = (D, C, B, A) is not a path, since(C, B) is not an edge, that is the direction of the edge e5 = (B, C) does not agree with the direction of the pathP1.
On the other hand P2 = (D, B, A) is a path from D to A, since (D, B) and (B, A) are edges. Thus A is reachable from D.
There is no path from C to any other node, so G is not strongly connected. However, G is unilaterally connected.
You can also go through a few more amazing blog links below related to Data Structure:
What is a strongly connected graph? / How do you know if a graph is strongly connected…
Graph: Types of the graph in data structure…
AVL Tree In Data Structure…
What is a tree in the data structure…
What is compaction in memory management…
What is garbage collection and how does it work…
Dynamic Memory Management…
Josephus problem & Circular linked list…
What is a circular linked list…
What are the linked lists in the data structure and their types…
What is the priority queue with an example…
the difference between stack and queue…
What is meant by backtracking in the data structure…
Conclusion:
Using this graph we have learned How to know if a graph is strongly connected? What is a strongly and weakly connected graph? How do you create a strongly connected graph? What is the number of strongly connected components in this graph? Strongly connected graph example.|What is a strongly connected graph|
In the case of any queries, you can write to us at a5theorys@gmail.com we will get back to you ASAP.
Hope! you would have enjoyed this post about What is a strongly connected graph.
Please feel free to give your important feedback in the comment section below.
Have a great time! Sayonara!


