Radix Sort Algorithm In Data Structure With Example.
Hello Friends, in this blog post(Radix Sort Algorithm In Data Structure With Example) I am going to let you know about the Radix Sort in Data Structure. Radix sort is a method that many people intuitively use when alphabetizing a large list of names.
In this blog post-Radix Sort Algorithm In Data Structure With Example’, we are going to explore What the radix sort is used for. Which sorting technique Cannot be used in radix sort? Is radix sort and bucket sort the same? What are the 3 types of sorting?
What is the radix sort used for?|Radix Sort Algorithm In Data Structure With Example?
radix sort is known as an integer sorting algorithm and it sorts the data by integer key.
It creates the grouping of keys by individual digits and uses them to find out the significant position and value.
For example, radix sorts the array of a number with the use of the counting sort algorithm|Radix Sort Algorithm In Data Structure With Example|
Which sorting technique Cannot be used in radix sort?
As we know radix sort is used to sort the data of positive integers.
So we can not use radix sort for sorting the non-integer value(ex: number with decimal)
Is radix sort and bucket sort the same?
They both are like cousins. But the difference is that Bucket sort goes from MSD(most significant digit) to LSD(Least significant digit), whereas radix sort can go in either direction from MSD to LSD or LSD to MSD.
Here the Radix is 26, the 26 letters of the alphabet specifically, the list of names is first sorted according to the first letter of each name.
That is, the names are arranged in 26 classes, where the first class consists of those names that begin with ‘A’, the second class consists of those names that begin with ‘B’, and so on.
During the second pass, each class is alphabetized according to the second letter of the name, and so on.
If no name contains, for example, more than 12 letters, the names are alphabetized with at most 12 passes.
The radix sort is the method used by a card sorter. A card sorter contains 13 receiving pockets labeled as follows-
9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 11, 12, R (reject)
Each pocket other than R corresponds to a row on a card in which a hole can be punched.
Decimal numbers, where the radix is 10, are punched in an obvious way and hence use only the first 10 pockets of the sorter.
The sorter uses a radix reverse-digit sort on numbers.
It means that suppose a card sorter is given a collection of cards where each card contains a 3-digit number punched in columns 1 to 3.
The cards are first sorted according to the unit’s digit.
On the second pass, the cards are sorted according to the tens digit. On the third and last pass, the cards are sorted according to the hundreds of digits.
The following example illustrates this – suppose 9 cards are punched as follows-
348, 143, 361, 423, 538, 128, 321, 543, 366
Given to a card sorter, the numbers are sorted in three phases, as shown in fig 1, fig 2, and fig 3 respectively.
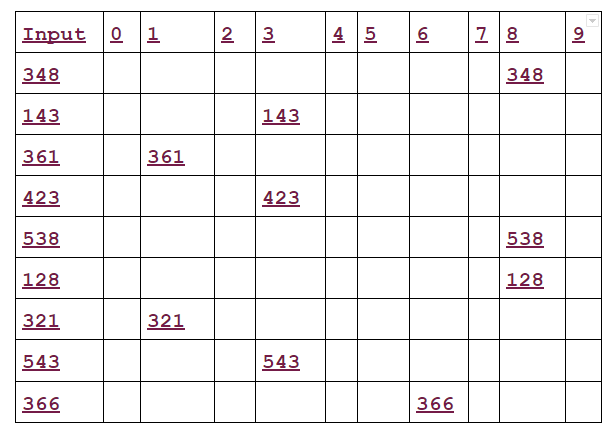
In the first pass of radix sort, the unit digits are sorted into pockets.
The pockets are pictured upside down, so 348 is at the bottom of pocket 8.
The cards are collected pocket by pocket, from pocket 9 to pocket 0.
Note that 361 will now be at the bottom of the pile and 128 at the top of the pile. the cards are now reinput to the sorter.
If you still could not understand the first pass format and value insertion then here I will explain it to you in very simple language.
first, here we have to sort the three-digit number so we will have a total of three passes to sort out the list.
Further, we make a table of 10×10, meaning 10 rows and 10 columns because we are sorting the decimal number.
Now as we know in the first pass, we see the unit digit number to place the number in the table.
Our first number is 348, In this number 8 is our unit digit number now we insert this number in the 8th column corresponding to 348 rows. As you can see this number is inserted in Fig 1.

In the second pass of radix sort, the tens digits are sorted into pockets.
Again the cards are collected pocket by pocket and reinput to the sorter.
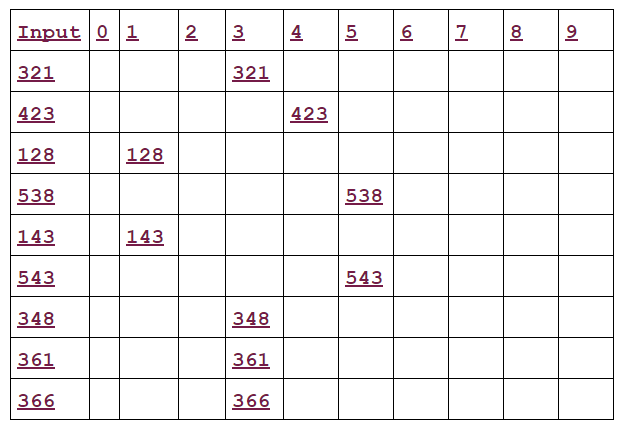
In the third and final pass of the radix sort, the hundreds of digits are sorted into pockets.
When the cards are collected after the third pass, the numbers are in the following order.
128, 143, 321, 348, 361, 366, 423, 538, 543
Thus the cards are now sorted.
Please go through the below extensive blog link related to the sorting techniques:
Sorting Algorithm And Their Time Complexity In Data Structure.
What is meant by the Shell sort in data structure?
Merge Sort In Data Structure/ What is merge sorting in data structure?
What is a quick sort of data structure?/ How do you write a quick sort?
Bubble Sort In Hindi In Data Structure/ What is bubble sort for example?/ Bubble Sort Kya Hai?
Insertion Sort In Hindi/ insertion sort step by step/ Insertion sort kya hai?
Searching In Data Structure/ What is the searching in data structure?
Conclusion:
Within this blog post(Radix Sort Algorithm In Data Structure With Example), we have gone through What is radix sort used for, Which sorting technique Cannot be used in radix sort, Is radix sort and bucket sort the same, What are the 3 types of sorting.
In the case of any queries, you can write to us at a5theorys@gmail.com we will get back to you ASAP.
Hope! you would have enjoyed this post about ‘Radix Sort Algorithm In Data Structure With Example‘.
Please feel free to give your important feedback in the comment section below|Radix Sort Algorithm In Data Structure With Example|
Have a great time! Sayonara!


